5.0 Introduction
5.0.1 Pourquoi devrais-je suivre ce module?
Bienvenue aux Systèmes Numériques !
Et devinez quoi ? C’est une adresse IPv4 32 bits d’un ordinateur dans un réseau : 11000000.10101000.00001010.00001010. Il est montré en binaire. C’est l’adresse IPv4 du même ordinateur en décimal pointillé : 192.168.10.10. Avec lequel préférez-vous travailler ? Les adresses IPv6 sont 128 bits ! Pour rendre ces adresses plus faciles à gérer, IPv6 utilise un système hexadécimal de 0-9 et les lettres A-F.
En tant qu’administrateur réseau, vous devez savoir comment convertir des adresses binaires en adresses décimales pointillées et décimales pointillées en binaires. Vous aurez également besoin de savoir comment convertir décimal pointillé en hexadécimal et vice versa. ( Conseil: Vous devez encore avoir vos compétences en conversion binaire pour que cela fonctionne.
Étonnamment, ce n’est pas si difficile quand vous apprenez quelques trucs. Ce module contient une activité appelée le jeu binaire qui vous aidera vraiment à démarrer. Alors, pourquoi attendre ?
5.0.2 Qu’est-ce que je vais apprendre dans ce module?
Titre du module: Systèmes numériques
Objectif du module: Calculer des nombres entre les systèmes décimaux, binaires et hexadécimaux.
| Titre du rubrique | Objectif du rubrique |
|---|---|
| Système binaire | Convertir des nombres entre les systèmes décimaux et binaires. |
| Système hexadécimal | Convertir des nombres entre les systèmes décimaux et hexadécimaux. |
5.1 Système binaire
5.1.1 Adresses binaires et IPv4
Les adresses IPv4 commencent comme binaires, une série de 1 et 0 seulement. Ceux-ci sont difficiles à gérer, de sorte que les administrateurs réseau doivent les convertir en décimal. Cette rubrique vous montre quelques façons de le faire.
Le format binaire est un système de numération utilisant les chiffres 0 et 1 qui sont appelés des bits. Le système de numération décimal utilise 10 chiffres, de 0 à 9.
Il est important de comprendre le système binaire puisque les hôtes, les serveurs et les périphériques réseau utilisent l’adressage binaire. Plus précisément, ils utilisent des adresses IPv4 binaires, comme le montre la figure, pour s’identifier mutuellement.
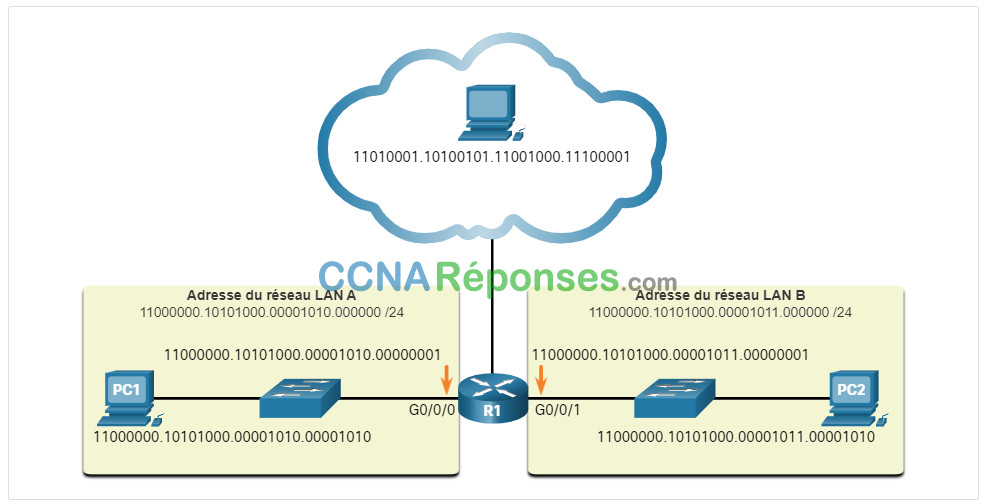
Chaque adresse est une chaîne de 32 bits divisée en quatre parties appelées octets. Chaque octet contient 8 bits séparés par un point. Par exemple, sur la figure, l’adresse IPv4 de PC1 est 11000000.10101000.00001010.00001010. L’adresse de sa passerelle par défaut serait celle de l’interface Gigabit Ethernet de R1, 11000000.10101000.00001010.00000001.
Le binaire fonctionne bien avec les hôtes et les périphériques réseau. Cependant, il est très difficile pour les humains de travailler avec.
Pour simplifier leur utilisation, les adresses IPv4 sont souvent exprimées en notation décimale pointillée. L’adresse IPv4 192.168.10.10 est attribuée à PC1, et son adresse de passerelle par défaut est 192.168.10.1, comme le montre la figure.
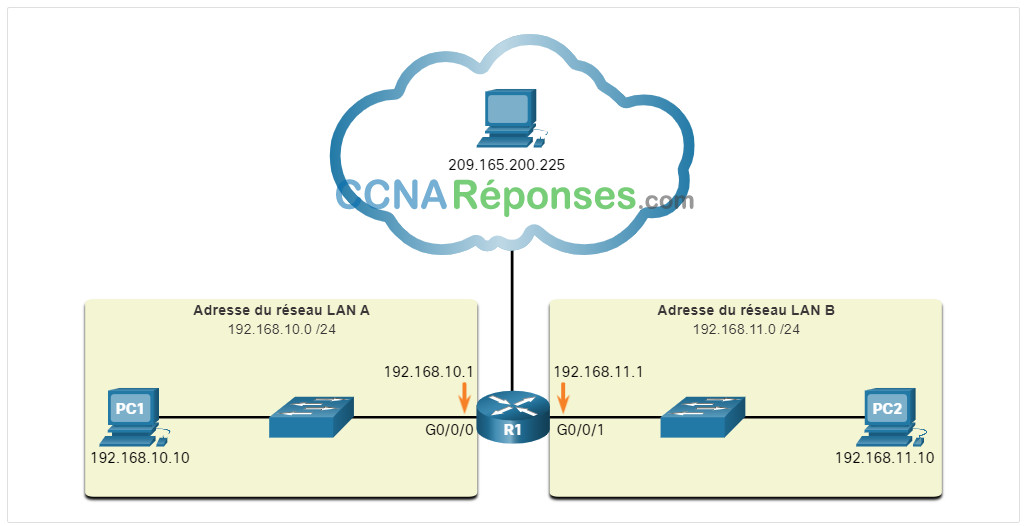
Pour bien comprendre l’adressage réseau, il est important de connaître l’adressage binaire et de s’entraîner à convertir des adresses IPv4 entre le format binaire et le format décimal à point. Cette section traite de la conversion entre les systèmes de numération en base 2 (binaire) et en base 10 (décimale).
5.1.3 Notation de position binaire
Pour apprendre à convertir du binaire en décimal, il faut comprendre la notation positionnelle. En numération pondérée, un chiffre représente différentes valeurs, selon la « position » qu’il occupe dans la séquence de chiffres. Vous connaissez déjà le système de numération le plus courant : le système de notation décimale (base 10).
Le système de notation positionnelle décimale fonctionne comme décrit dans le tableau.
| Base | 10 | 10 | 10 | 10 |
|---|---|---|---|---|
| Position du nombre | 3 | 2 | 1 | 0 |
| Calcul | (103) | (102) | (101) | (100) |
| Valeur de position | 1000 | 100 | 10 | 1 |
Les puces suivantes décrivent chaque ligne du tableau.
- Rangée 1, Radix est la base du nombre. Le système de notation décimale est en base de 10, donc le radix est 10.
- Rangée 2, Position en nombre, considère la position du nombre décimal commençant par, de droite à gauche, 0 (1ère position), 1 (2ème position), 2 (3ème position), 3 (4ème position). Ces chiffres représentent également la valeur exponentielle utilisée pour calculer la valeur de position dans la 4ème ligne.
- Rangée 3 calcule la valeur de la position en prenant le radix et en l’augmentant de la valeur exponentielle de sa position dans la rangée 2.
Remarque: n0est = 1. - La valeur de position de la rangée 4 représente des unités de milliers, de centaines, de dizaines et d’unités.
Pour utiliser la numération pondérée, utilisez la valeur pondérée de chaque chiffre. L’exemple du tableau illustre comment la notation positionnelle est utilisée avec le nombre décimal 1234.
| Milliers | Centaines | Dizaines | Unités | |
|---|---|---|---|---|
| Valeur positionnelle | 1000 | 100 | 10 | 1 |
| Nombre décimal (1234) | 1 | 2 | 3 | 4 |
| Calcule | 1 x 1000 | 2 x 100 | 3 x 10 | 4 x 1 |
| Ajoutez-les… | 1000 | + 200 | + 30 | + 4 |
| Le résultat | 1234 | |||
En revanche, la notation positionnelle binaire fonctionne comme décrit dans le tableau.
| Base | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
|---|---|---|---|---|---|---|---|---|
| Position du nombre | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| Calcule | (27) | (26) | (25) | (24) | (23) | (22) | (21) | (20) |
| Valeur de position | 128 | 64 | 32 | 16 | 8 |
Les puces suivantes décrivent chaque rangée du tableau.
- Rangée 1, Radix est la base du nombre. Le système de notation binaire est en base de 2, donc le radix est 2.
- Rangée 2, Position en nombre, considère la position du nombre décimal commençant par, de droite à gauche, 0 (1ère position), 1 (2ème position), 2 (3ème position), 3 (4ème position). Ces chiffres représentent également la valeur exponentielle utilisée pour calculer la valeur de position dans la 4ème rangée.
- Rangée 3 calcule la valeur de la position en prenant le radix et en l’augmentant de la valeur exponentielle de sa position dans la rangée 2.
Remarque: n0est = 1. - La valeur de position de la rangée 4 représente les unités de un, deux, quatre, huit, etc.
L’exemple du tableau illustre comment un nombre binaire 11000000 correspond au nombre 192. Si la valeur binaire avait été 10101000, le nombre décimal correspondant serait 168.
| Valeur pondérée | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| Nombre binaire (11000000) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Calcule | 1 x 128 | 1 x 64 | 0 x 32 | 0 x 16 | 0 x 8 | 0 x 4 | 0 x 2 | 0 x 1 |
| Ajoutez-les… | 128 | + 64 | + 0 | + 0 | + 0 | + 0 | + 0 | + 0 |
| Le résultat | 192 | |||||||
5.1.5 Convertir les binaires en décimales
Pour convertir une adresse IPv4 binaire en équivalent décimal à point, divisez l’adresse IPv4 en quatre octets de 8 bits. Appliquez ensuite la valeur pondérée binaire au premier octet binaire et calculez.
Par exemple, supposons que 11000000.10101000.00001011.00001010 est l’adresse IPv4 binaire d’un hôte. Pour convertir l’adresse binaire en décimal, commencez par le premier octet, comme indiqué dans le tableau. Saisissez la valeur binaire à 8 bits sous la valeur pondérée de la première ligne, puis effectuez le calcul pour obtenir le nombre décimal 192. Ce résultat correspond au premier octet de la notation en décimale à point.
| Valeur positionnelle | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| Nombre binaire (11000000) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Calcule | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| Ajoutez-les… | 128 | + 64 | + 0 | + 0 | + 0 | + 0 | + 0 | + 0 |
| Le résultat | 192 | |||||||
Ensuite, convertissez le deuxième octet de 10101000 comme indiqué dans le tableau. Vous obtenez la valeur décimale 168, qui correspond au deuxième octet.
| Valeur positionnelle | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| Nombre binaire (10101000) | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| Calcule | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| Ajoutez-les… | 128 | + 0 | + 32 | + 0 | + 8 | + 0 | + 0 | + 0 |
| Le résultat | 168 | |||||||
Convertir le troisième octet de 00001011 comme indiqué dans le tableau.
| Valeur positionnelle | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| Nombre binaire (00001011) | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| Calcule | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| Ajoutez-les… | 0 | + 0 | + 0 | + 0 | + 8 | + 0 | + 2 | + 1 |
| Le résultat | 11 | |||||||
Convertir le quatrième octet de 00001010 comme indiqué dans le tableau. Ceci termine l’adresse IP et produit 192.168.11.10.
| Valeur positionnelle | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| Nombre binaire (00001010) | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| Calcule | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| Ajoutez-les… | 0 | + 0 | + 0 | + 0 | + 8 | + 0 | + 2 | + 0 |
| Le résultat | 10 | |||||||
5.1.7 Conversion de nombres décimaux en nombres binaires
Il est également important de comprendre comment convertir une adresse IPv4 décimale à point en son équivalent binaire. La table des valeurs pondérées binaires peut vous y aider.
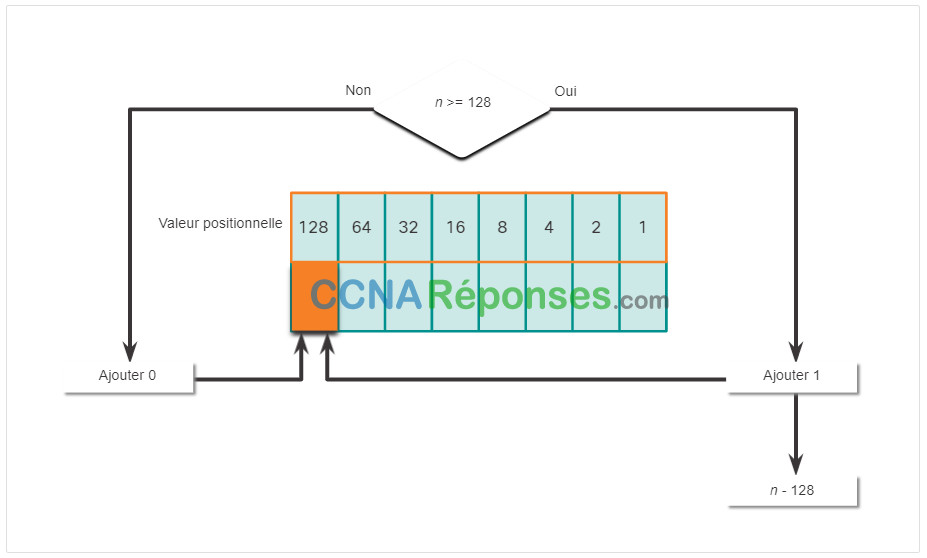
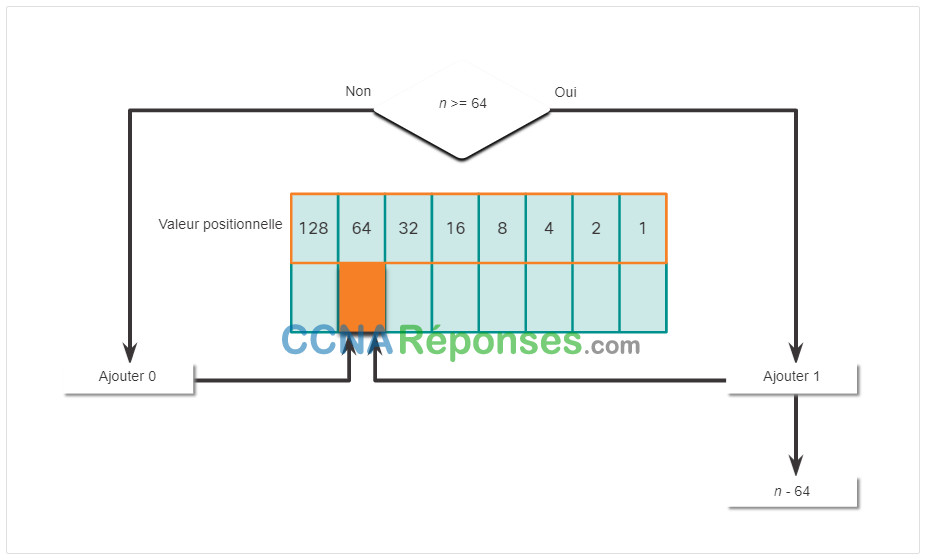
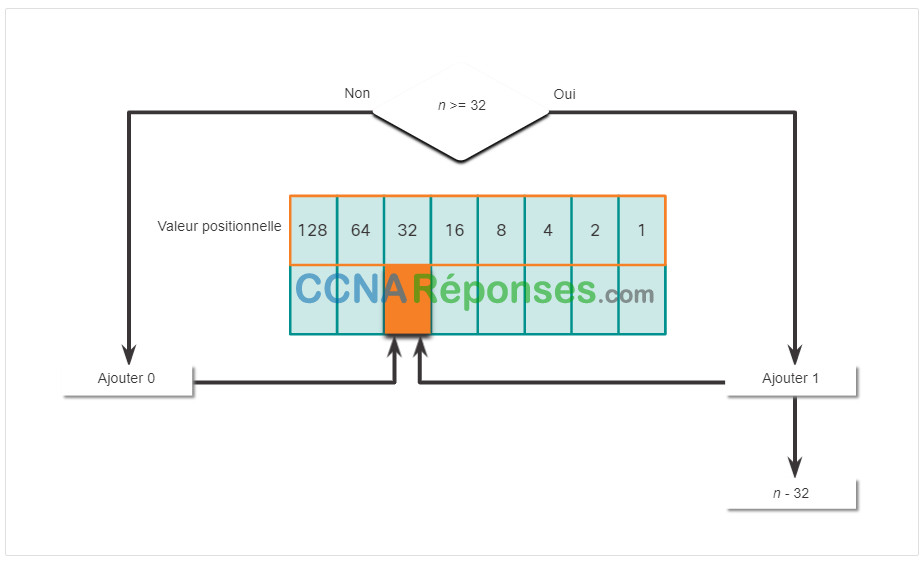
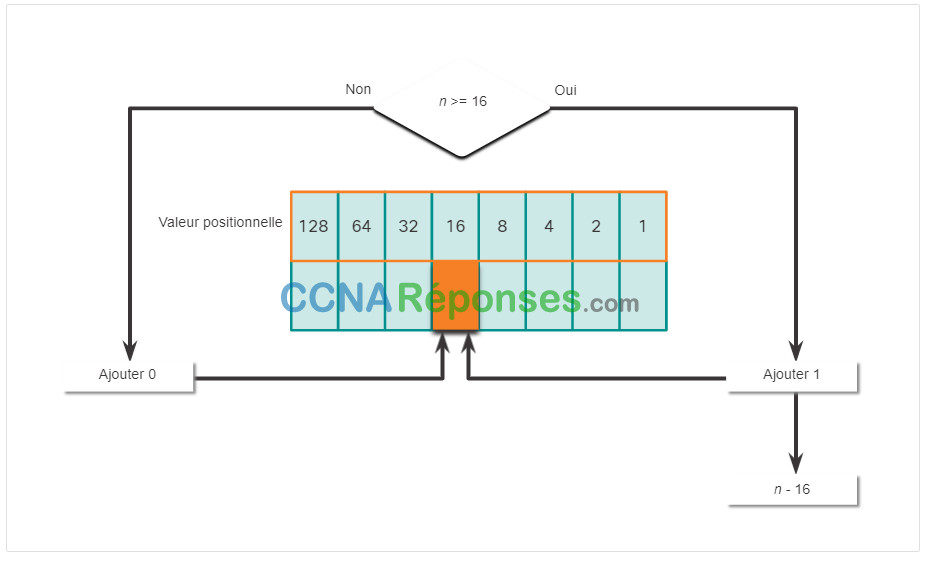
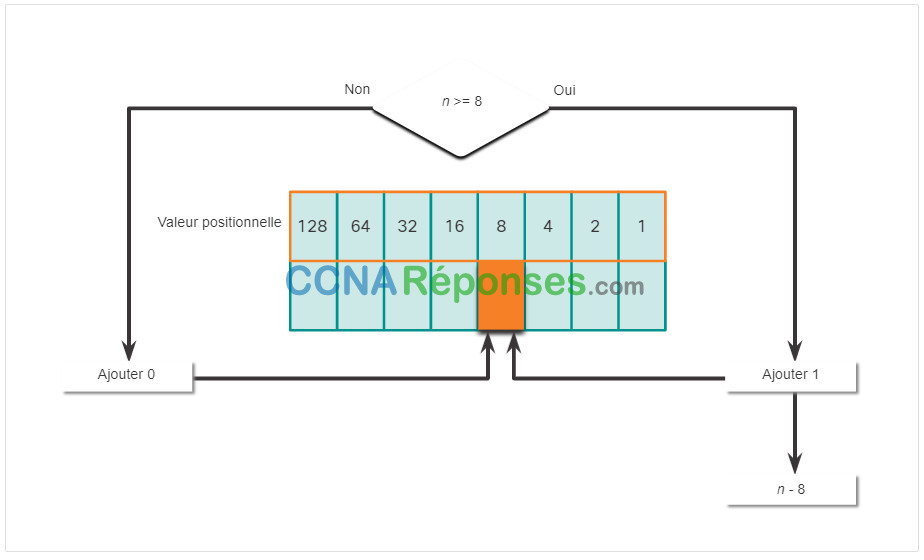
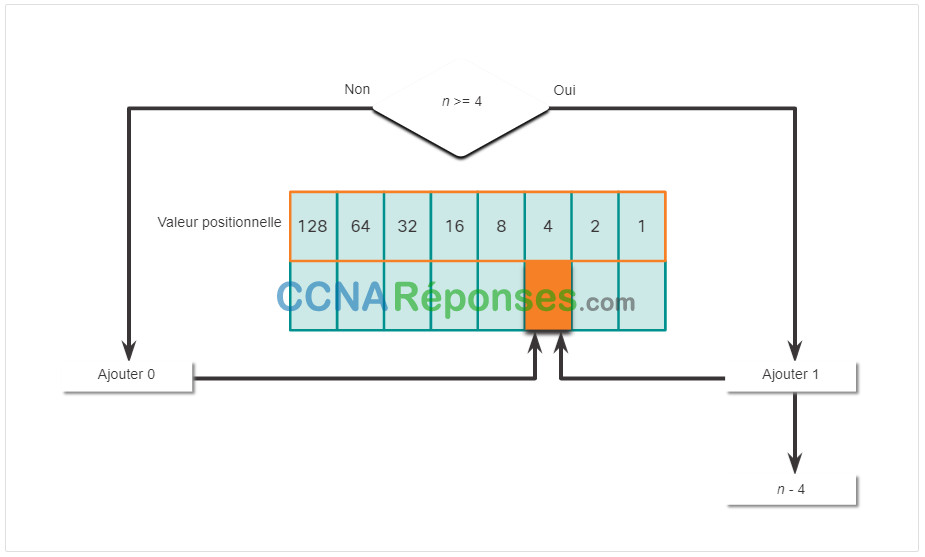
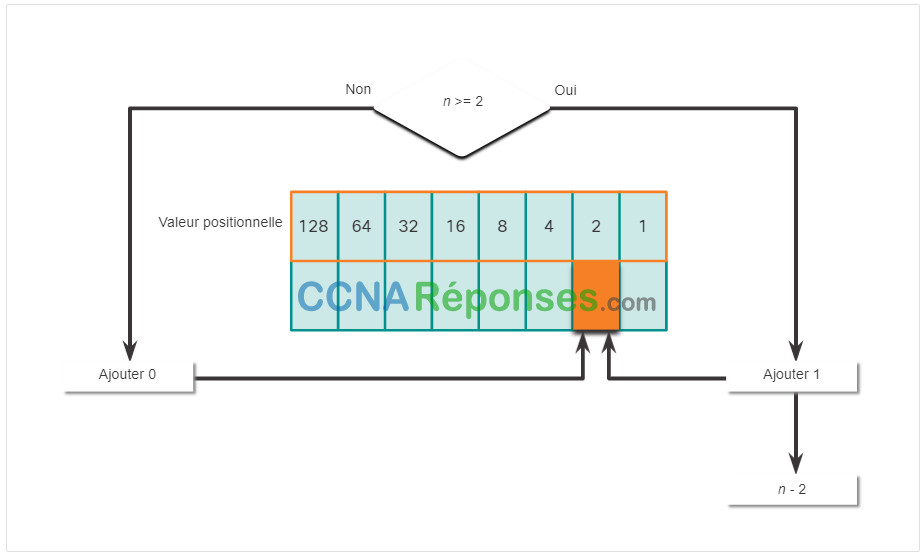
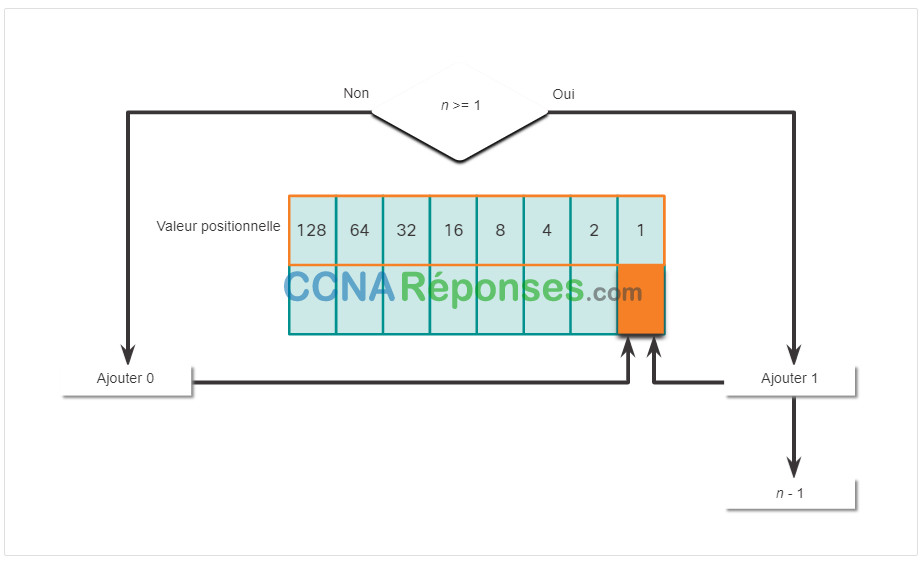
Cliquez sur chaque position à partir de 128 et travaillez votre chemin de gauche à droite jusqu’à la position 1.
Le nombre décimal de l'octet (n) est-il égal ou supérieur au bit le plus significatif (128) ?
- Si non, alors entrez le 0 binaire dans la valeur positionnelle 128.
- Si oui, alors ajoutez un 1 binaire dans la valeur positionnelle 128 et soustrayez 128 à partir du nombre décimal.
Le nombre décimal de l'octet (n) est-il égal ou supérieur au bit suivant le plus significatif (64) ?
- Si non, alors entrez le 0 binaire dans la valeur positionnelle 64.
- Si oui, alors ajoutez un 1 binaire dans la valeur positionnelle 64 et soustrayez 64 à partir du nombre décimal.
Le nombre décimal de l'octet (n) est-il égal ou supérieur au bit suivant le plus significatif (32) ?
- Si non, alors entrez le 0 binaire dans la valeur positionnelle 32.
- Si oui, alors ajoutez un 1 binaire dans la valeur positionnelle 32 et soustrayez 32 à partir du nombre décimal.
Le nombre décimal de l'octet (n) est-il égal ou supérieur au bit suivant le plus significatif (16) ?
- Si non, alors entrez le 0 binaire dans la valeur positionnelle 16.
- Si oui, alors ajoutez un 1 binaire dans la valeur positionnelle 16 et soustrayez 16 à partir du nombre décimal.
Le nombre décimal de l'octet (n) est-il égal ou supérieur au bit suivant le plus significatif (8) ?
- Si non, alors entrez le 0 binaire dans la valeur positionnelle 8.
- Si oui, alors ajoutez un 1 binaire dans la valeur positionnelle 8 et soustrayez 8 à partir du nombre décimal.
Le nombre décimal de l'octet (n) est-il égal ou supérieur au bit suivant le plus significatif (4) ?
- Si non, alors entrez le 0 binaire dans la valeur positionnelle 4.
- Si oui, alors ajoutez un 1 binaire dans la valeur positionnelle 4 et soustrayez 4 à partir du nombre décimal.
Le nombre décimal de l'octet (n) est-il égal ou supérieur au bit suivant le plus significatif (2) ?
- Si non, alors entrez le 0 binaire dans la valeur positionnelle 128.
- Si oui, alors ajoutez un 1 binaire dans la valeur positionnelle 2 et soustrayez 2 à partir du nombre décimal.
Le nombre décimal de l'octet (n) est-il égal ou supérieur au bit le plus significatif (1) ?
- Si non, alors entrez le 0 binaire dans la valeur positionnelle 1.
- Si oui, alors ajoutez un 1 binaire dans la valeur positionnelle 1 et soustrayez 1 à partir du nombre décimal.
5.1.8 Exemple de conversion décimal en binaire
Pour comprendre le processus, nous allons nous entraîner avec l’adresse IP 192.168.11.10.
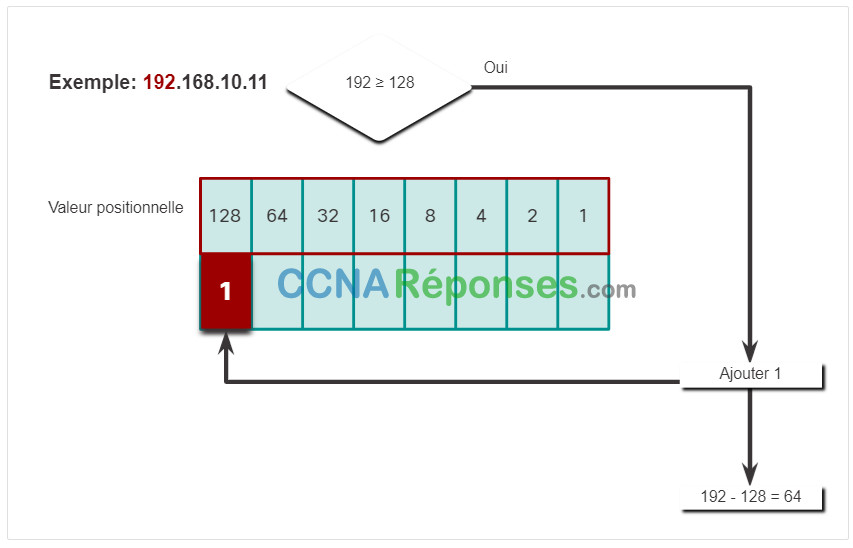
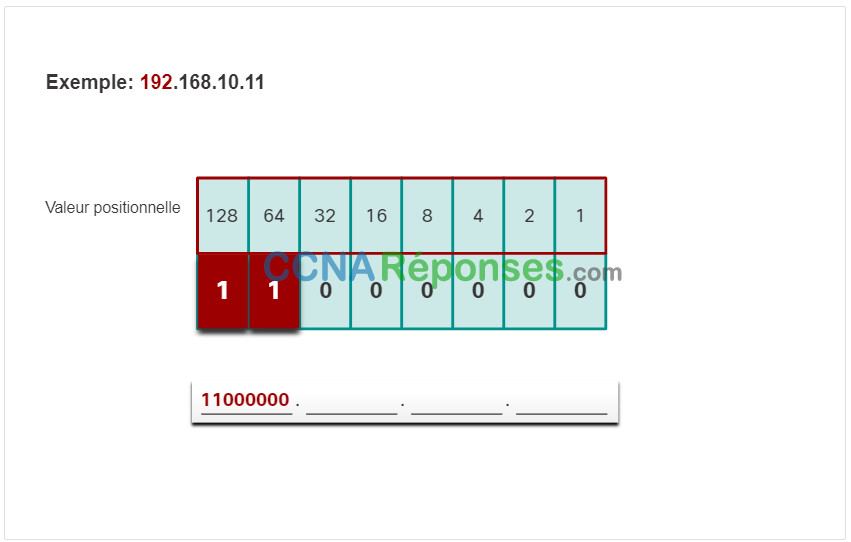
Le premier nombre d’octets 192 est converti en binaire en utilisant le processus de notation positionnelle expliqué précédemment.
Il est possible d’éviter les soustractions lorsque les nombres décimaux sont plus simples ou plus petits. Par exemple, remarquez qu’il est assez facile de calculer le troisième octet converti en un nombre binaire sans passer par le processus de soustraction (8 + 2 = 10). La valeur binaire du troisième octet est 00001010.
Le quatrième octet est 11 (8 + 2 + 1). La valeur binaire du quatrième octet est 00001011.
La conversion entre les valeurs binaires et décimales peut sembler compliquée au début, mais à force de pratique, elle vous paraîtra plus simple.
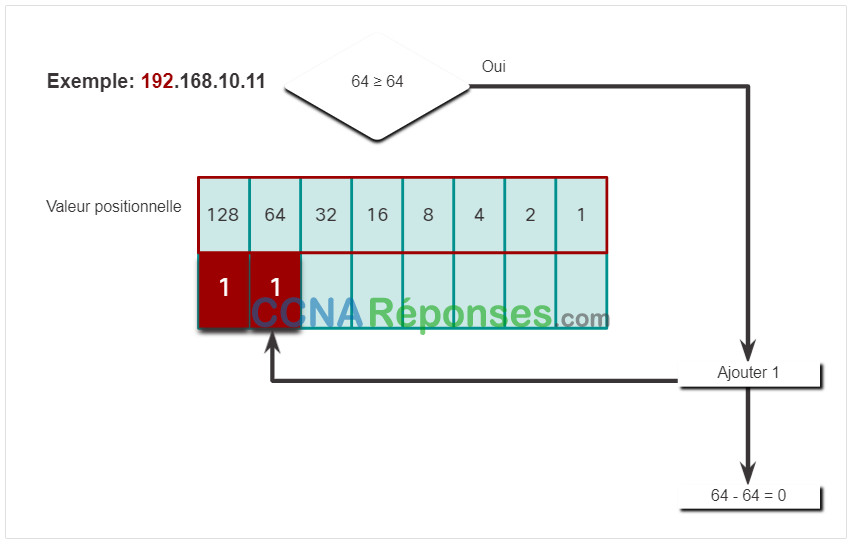
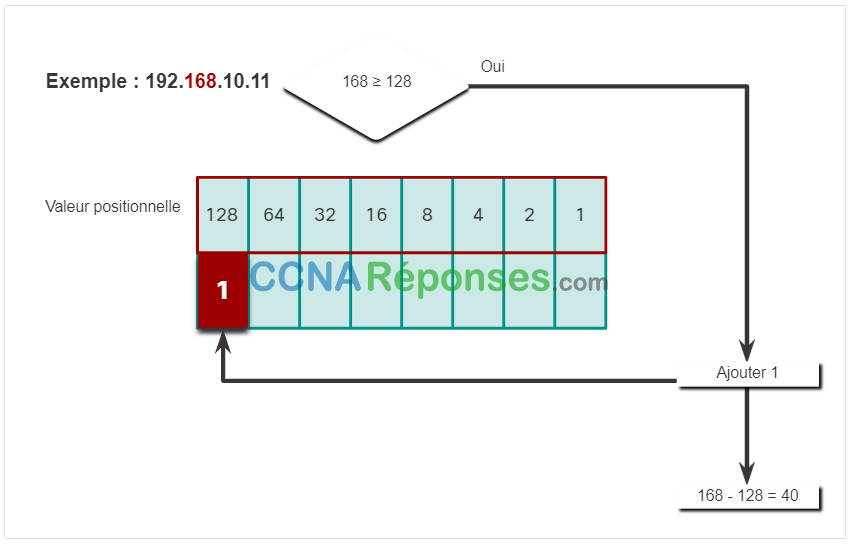
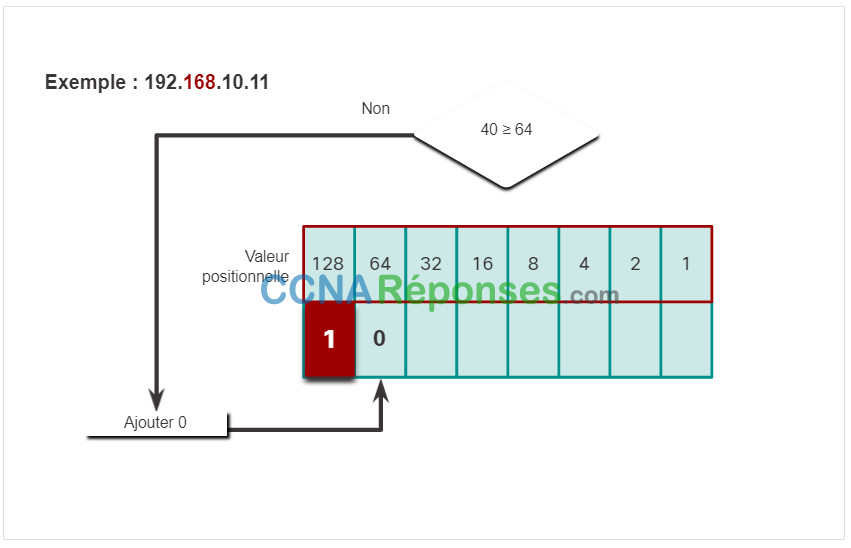
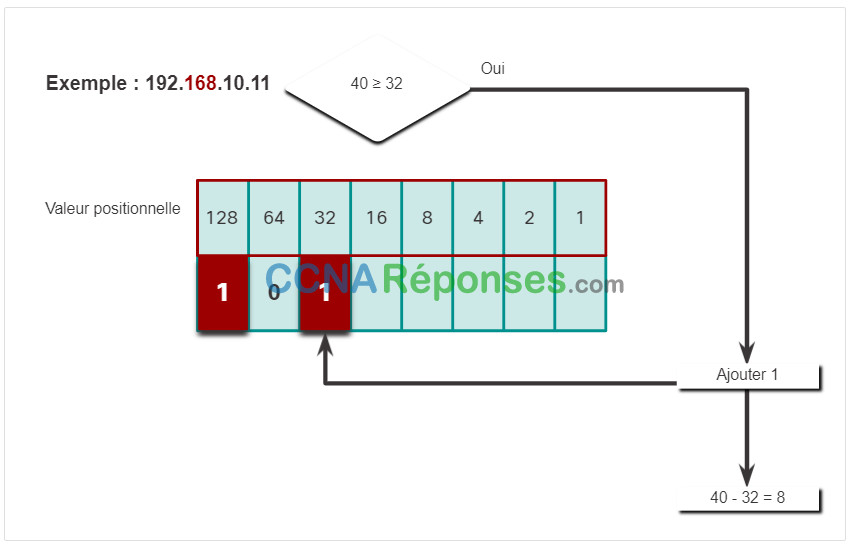
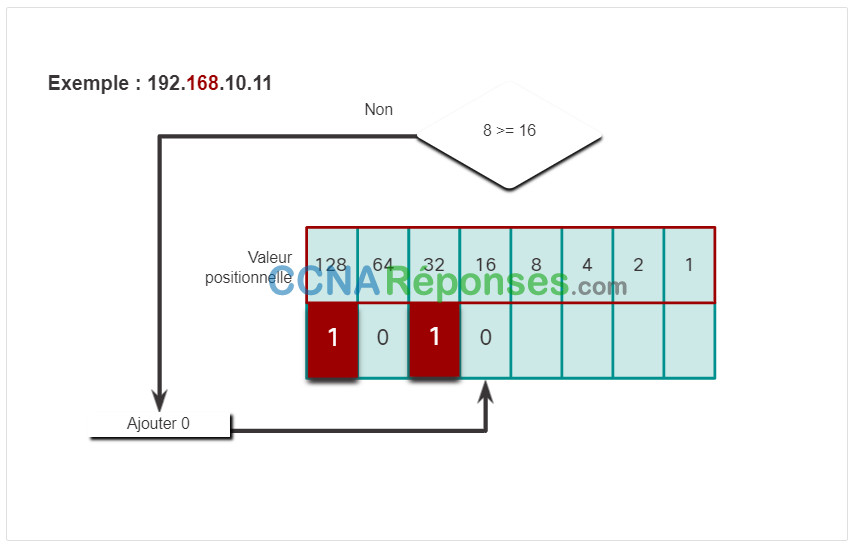
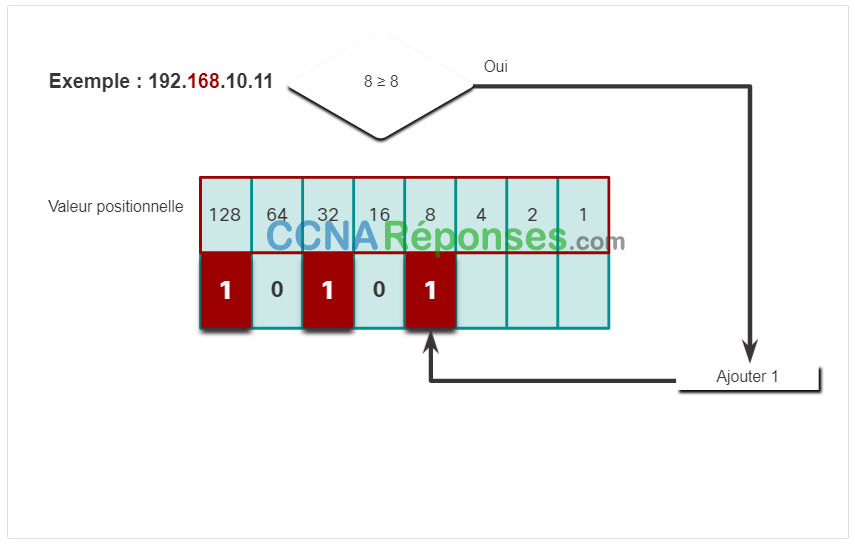
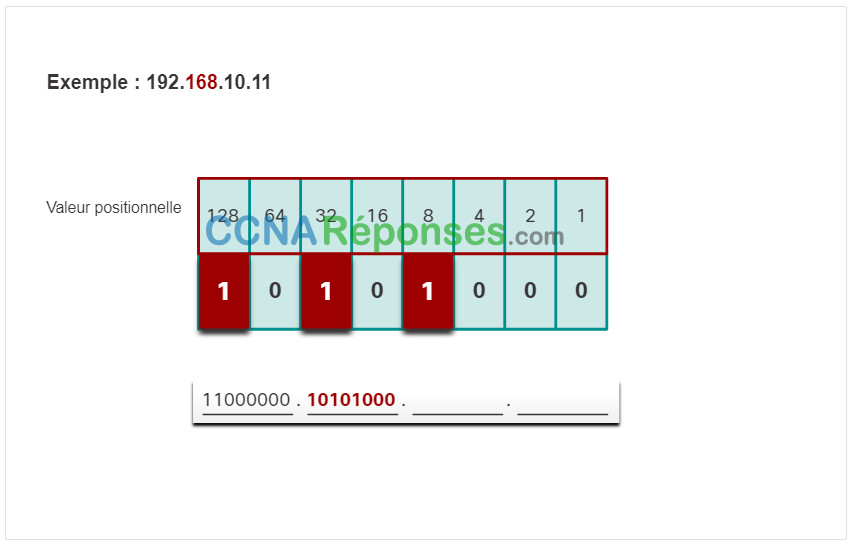
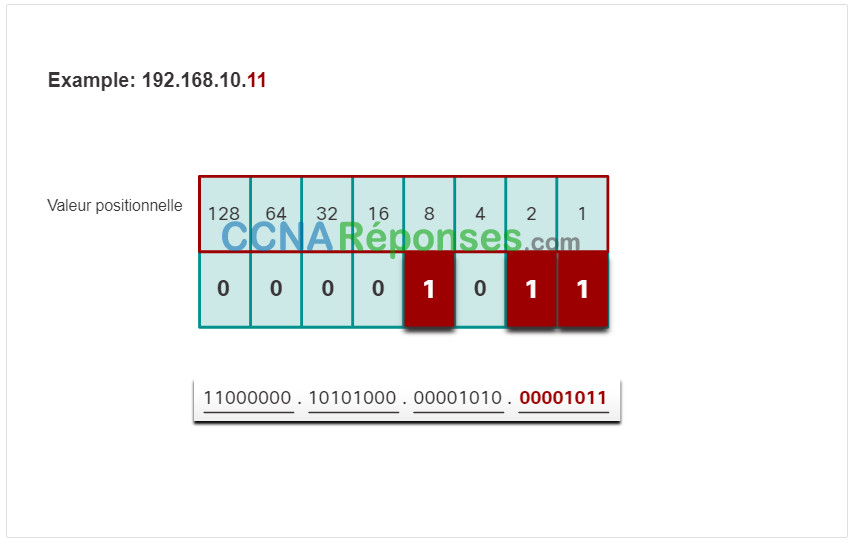
Cliquez sur chaque étape pour voir la conversion de l’adresse IP de 192.168.10.11 en binaire.
Le premier nombre d'octet 192 est-il égal ou supérieur au bit 128 d'ordre élevé?
- Oui, il est, donc ajouter un 1 à la valeur de position d'ordre élevé à une représentation 128.
- Retranchez ensuite 128 à 192 pour obtenir 64.
Le reste 64 est-il égal ou supérieur au bit 64 suivant d'ordre élevé ?
- Il est égal, donc ajoutez un 1 à la suivante valeur positionnelle d'ordre élevé.
Comme il n'y a pas de reste, entrez binaire 0 dans les valeurs de position restantes.
- La valeur binaire du premier octet est de 11000000.
Le deuxième nombre d'octet est-il 168 égal ou supérieur au bit d'ordre élevé 128 ?
- Oui, c'est le cas, donc ajoutez un 1 à la valeur de position d'ordre élevé pour représenter 128.
- Retranchez 128 de 168 pour obtenir un reste de 40.
Le reste est-il 40 égal ou supérieur au bit d'ordre supérieur suivant 64 ?
- Non, il ne s'agit donc pas d'entrer un 0 binaire dans la valeur positionnelle.
Le reste est-il 40 égal ou supérieur au bit d'ordre supérieur suivant 32 ?
- Oui, c'est le cas, donc ajoutez un 1 à la valeur de position d'ordre élevé pour représenter 32.
- Retranchez 32 de 40 pour obtenir un reste de 8.
Le reste est-il 8 égal ou supérieur au bit d'ordre supérieur suivant 16 ?
- Non, il n'est pas, par conséquent, entrez un binaire 0 dans la valeur positionnelle.
Le reste est-il 8 égal ou supérieur au bit d'ordre supérieur suivant 8 ?
- It is equal, therefore add a 1 à la valeur de position d'ordre supérieur suivant.
Comme il n'y a pas de reste, entrez binaire 0 dans les valeurs de position restantes.
- The binary value of the second octet is **10101000
La valeur binaire du troisième octet est 00001010.
La valeur binaire du quatrième octet est 00001011.
5.1.10 Exercice- Jeu binaire
C’est une façon amusante d’apprendre les nombres binaires pour le réseautage.
Jeu Link: https://learningnetwork.cisco.com/docs/DOC-1803
Vous devrez vous connecter à cisco.com pour utiliser ce lien. Il sera nécessaire de créer un compte si vous n’en avez pas déjà un.
5.1.11 Adresses IPv4
Comme mentionné au début de cette rubrique, les routeurs et les ordinateurs ne comprennent que le binaire, tandis que les humains travaillent en décimal. Il est important pour vous d’acquérir une compréhension approfondie de ces deux systèmes de numération et de leur utilisation dans le réseautage.
Cliquez sur chaque bouton pour opposer l’adresse décimale pointillée et l’adresse 32 bits.
192.168.10.10 est une adresse IP attribuée à un ordinateur.
Cette adresse se compose de quatre octets différents.
L'ordinateur stocke l'adresse sous forme de flux de données complet de 32 bits.
5.2 Système hexadécimal
5.2.1 Adresses hexadécimales et IPv6
Maintenant, vous savez comment convertir binaire en décimal et décimal en binaire. Vous avez besoin de cette compétence pour comprendre l’adressage IPv4 dans votre réseau. Mais vous êtes tout aussi susceptible d’utiliser des adresses IPv6 dans votre réseau. Pour comprendre les adresses IPv6, vous devez pouvoir convertir hexadécimal en décimal et vice versa.
Le système décimal est en base dix et le système hexadécimal est en base seize. Le système des nombres en base seize utilise les chiffres 0 à 9 et les lettres A à F. La figure montre les valeurs décimales et hexadécimales équivalentes pour les binaires 0000 à 1111.
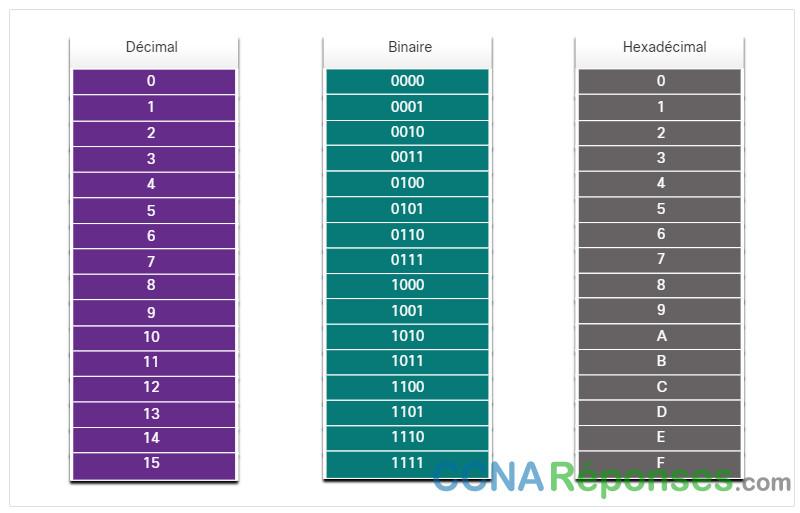
Le binaire et l’hexadécimal fonctionnent bien ensemble car il est plus facile d’exprimer une valeur sous forme d’un seul chiffre hexadécimal que sous forme de quatre bits binaires.
Le système de numération hexadécimale est utilisé en réseau pour représenter les adresses IP Version 6 et les adresses MAC Ethernet.
Les adresses IPv6 ont une longueur de 128 bits et chaque 4 bits est représenté par un seul chiffre hexadécimal ; pour un total de 32 valeurs hexadécimales. Les adresses IPv6 ne sont pas sensibles à la casse et peuvent être notées en minuscules ou en majuscules.
Comme le montre la figure, le format préféré pour écrire une adresse IPv6 est x:x:x:x:x:x:x:x, chaque “x” étant constitué de quatre valeurs hexadécimales. Pour faire référence aux 8 bits d’une adresse IPv4, nous utilisons le terme « octet ». Dans IPv6, un hextet est le terme non officiel utilisé pour désigner un segment de 16 bits ou quatre valeurs hexadécimales. Chaque “x” est un simple hextet, 16 bits, ou quatre chiffres hexadécimaux.
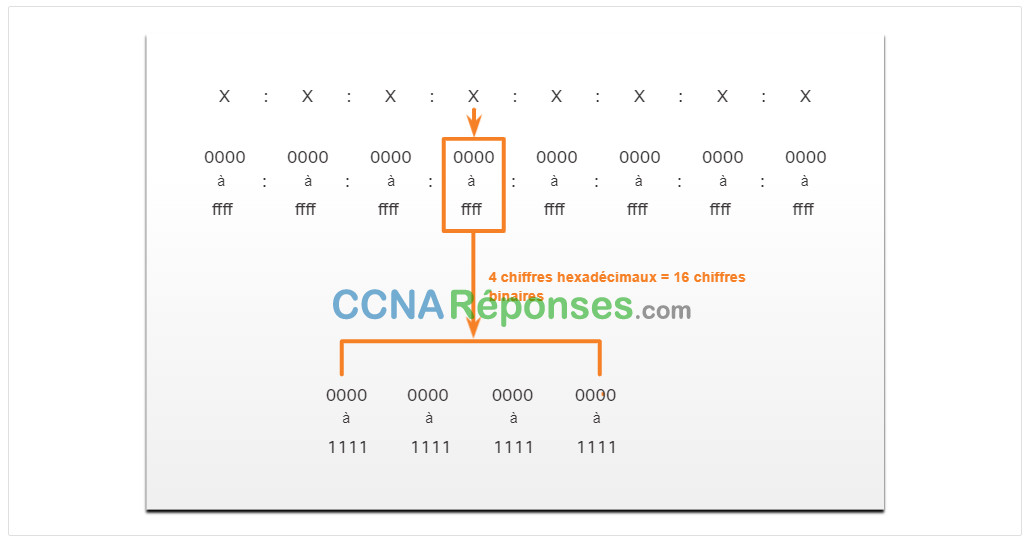
L’exemple de topologie de la figure affiche les adresses hexadécimales IPv6.
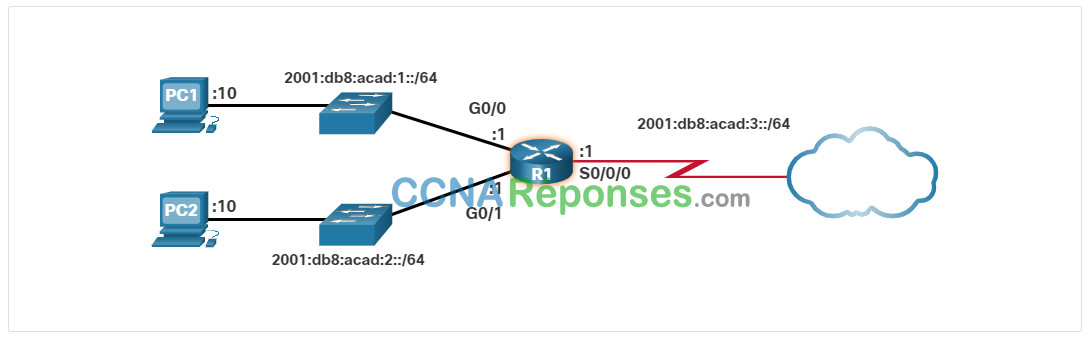
5.2.3 Conversions hexadécimale en décimale
La conversion de nombres décimaux en valeurs hexadécimales est simple. Suivez les étapes indiquées:
- Convertir le nombre décimal en chaînes binaires 8 bits.
- Divisez les chaînes binaires en groupes de quatre en partant de la position à droite.
- Convertissez chacun des quatre nombres binaires en leur équivalent hexadécimal.
L’exemple fournit les étapes de conversion de 168 en hexadécimal.
Par exemple, 168 converti en hexadécimal en utilisant le processus en trois étapes.
- 168 en binaire est 10101000.
- 10101000 dans deux groupes de quatre chiffres binaires est 1010 et 1000.
- 1010 est hexadécimal A et 1000 est hexadécimal 8.
Réponse: 168 est A8 en hexadécimal.
5.2.4 Conversion hexadécimale en décimale
La conversion de nombres hexadécimaux en valeurs décimales est également simple. Suivez les étapes indiquées :
- Convertir le nombre hexadécimal en chaînes binaires 4 bits.
- Créez un regroupement binaire 8 bits à partir de la position la plus à droite.
- Convertissez chaque regroupement binaire 8 bits en chiffres décimaux équivalents.
Cet exemple fournit les étapes de conversion de D2 en décimal.
- D2 dans les chaînes binaires 4 bits est 1101 et 0010.
- 1101 et 0010 est 11010010 dans un groupe 8 bits.
- 11010010 en binaire équivaut à 210 en décimal.
Réponse: D2 en hexadécimal est de 210 en décimal.
5.3 Module pratique et questionnaire
5.3.1 Qu’est-ce que j’ai appris dans ce module?
Système binaire
Le format binaire est un système de numération utilisant les chiffres 0 et 1 qui sont appelés des bits. En revanche, le système de numération décimale est constitué de 10 chiffres composés des nombres 0 – 9. Il est important que nous comprenions le binaire car les hôtes, les serveurs et les dispositifs de réseau utilisent l’adressage binaire, en particulier les adresses IPv4 binaires, pour s’identifier les uns les autres. Vous devez connaître l’adressage binaire et comment convertir entre les adresses IPv4 décimales binaires et pointillées. Cette rubrique présentait quelques façons de convertir décimal en binaire et binaire en décimal.
Système hexadécimal
Le système décimal est en base dix et le système hexadécimal est en base seize. Le système de numération hexadécimale utilise les nombres 0 à 9 et les lettres A à F. Le système de numération hexadécimale est utilisé en réseau pour représenter les adresses IPv6 et les adresses MAC Ethernet. Les adresses IPv6 ont une longueur de 128 bits et chaque 4 bits est représenté par un seul chiffre hexadécimal ; pour un total de 32 valeurs hexadécimales. Pour convertir hexadécimal en décimal, vous devez d’abord convertir l’hexadécimal en binaire, puis convertir le binaire en décimal. Pour convertir décimal en hexadécimal, vous devez également d’abord convertir la décimale en binaire.
